Making Disk Sources
Start with the developed gaussian process method for making a spheroid.
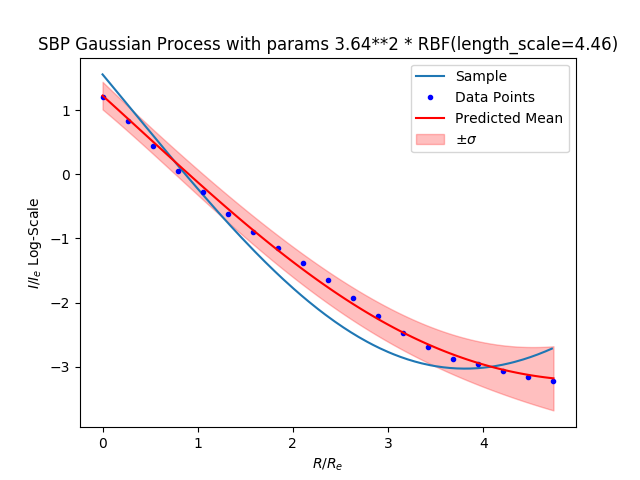
To change the spheroid source into a disk source we use a transformation matrix. Our new disk source will have an axis ratio of 0.5. To find the the major and minor axis, solve:
where $r$ is the effective radius in pixel units. $a$ and $b$ are used to make the transformation matrix which is an affine transformation:
Where $M_{scale}$ is a scaling matrix with a in the [0,0] location and b in the [1,1] location. $M_{origin}$ and $M_{center}$ are translation matrices that move to origin and then restore it.
Then change the axis ratio of the spheroid using the following transformation matrix:
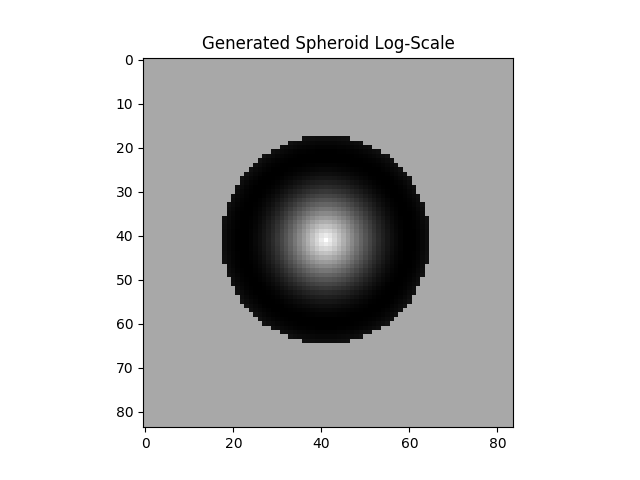
After applying the affine transformation the disk object looks like this:
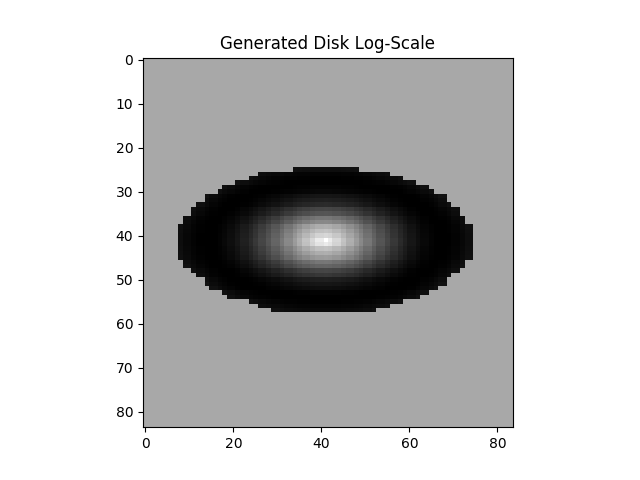
To confirm that the new image has the properties intended, the axis ratio can be measured directly from the image. We intended an axis ratio of 0.5 anf the measured axis ratio is 0.4956688764680927.
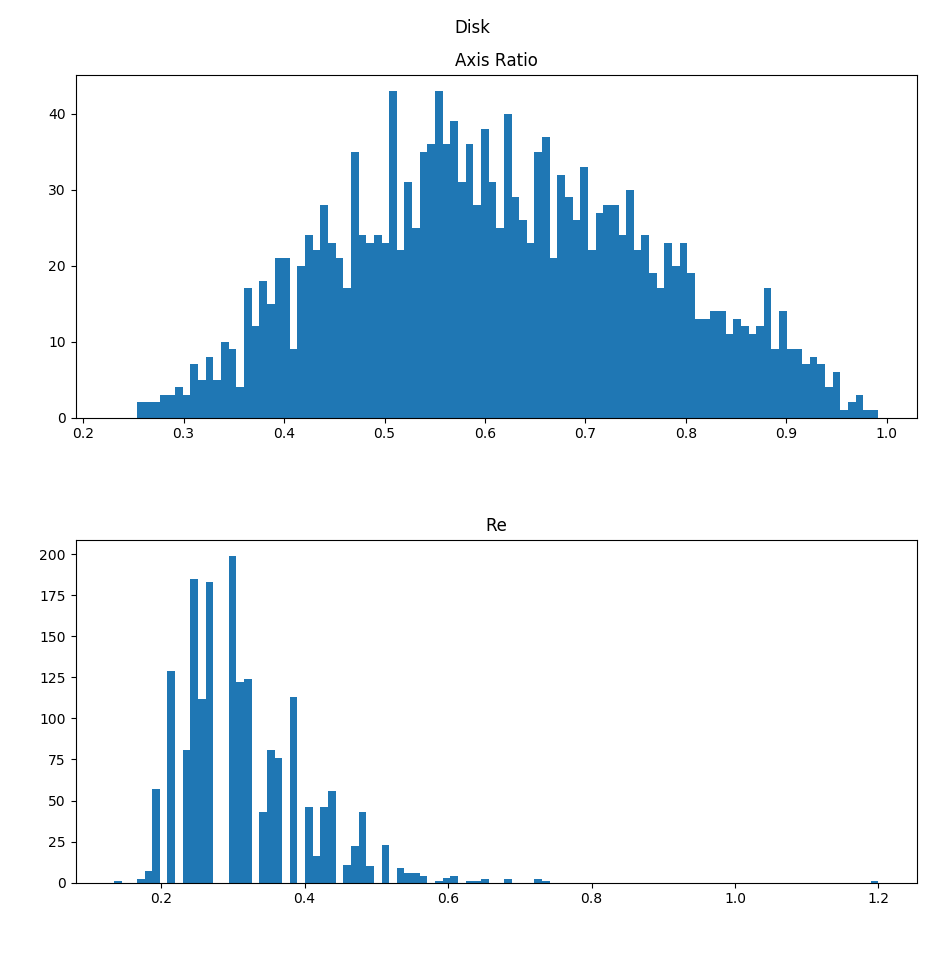
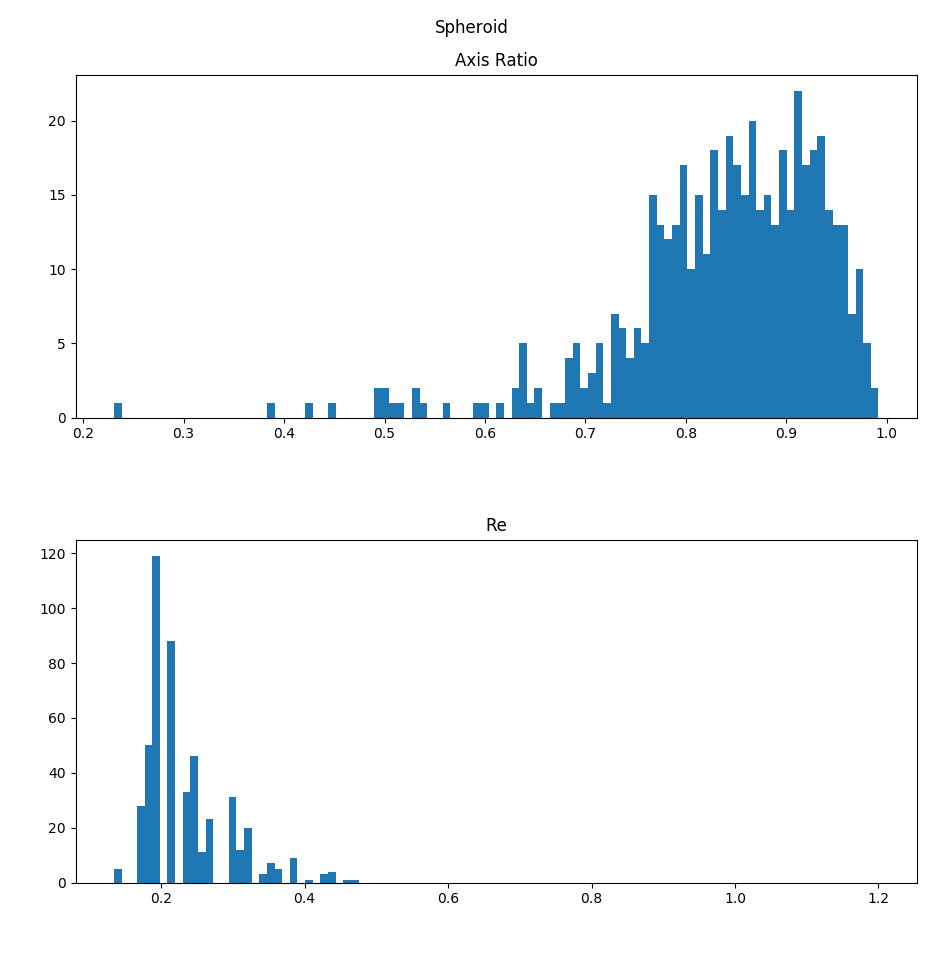
Update the Axis Ratio and Effective Radius Binning
I changed the numer of bins to 100 and also set the bounds for the binning to be shared between disks and spheroids for comparison. The new histograms look like this: