To create more accurate synthetic images for training the model we fit all the source images to a Sersic profile. Equation we use to define the Sersic profile is:
Where $m=1$ defines an exponential disk profile, $m=4$ defines a De Vaucouleurs spheroid profile, and $b_m=2m-0.324$
The parameters we want to fit are $I_e$ and $R_e$. Which will be optimized using fmin from scipy.optimize
import numpy as np
def sersic(Ie, Re, R, m):
bm = 2.0*m - 0.324
return Ie * np.exp(-bm * ((R/Re)**(1.0/m) - 1.0))
def get_surface_brightness_profile(img):
"""
img: a two dimensional array, dims (84,84)
"""
pix = 0.06 # arcseconds/pixel
n_bin = 100
center_dist = np.sqrt((0.5*84)**2 + (0.5*84)**2)
r_bin = .06 * center_dist * np.arange(bins) / float(bins)
I_bin = np.zeros(n_bin, dtype=float)
norm_bin = np.zeros(n_bin, dtype=float)
for i in range(nx):
for j in range(ny):
ix = np.abs(0.5*nx - i)
iy = np.abs(0.5*ny - j)
R = np.sqrt(ix*ix + iy*iy) * pix
idx = bisect.bisect_left(r_bin,R)-1
if((idx<n_bin-1) & (idx>0)):
I_bin[idx] += img[i,j]
norm_bin[idx] += 1.0
ip = np.where(norm_bin>0)[0]
I_bin[ip]/=norm_bin[ip]
return (r_bin, I_bin)
def sersic_optimize(x, m, y):
"""
x: an indexed object with two items Ie=x[0], Re=[1]
m: the m param for the sersic profile
y: the measured surface brightness profile of the object
"""
pix = .06 # arc/pixel
bins = 100 # number of bins
center_dist = np.sqrt((0.5*84)**2 + (0.5*84)**2)
r = .06 * center_dist * np.arange(bins) / float(bins)
# get the sersic profile for Ie = x[0] and Re = x[1]
s = sersic(x[0], x[1], r, m)
# return the squared error
return ((s[y>0]-y[y>0])**2).mean()
An example of usage for GDS_deep2_10016(disk) in the z band:
Original Image:
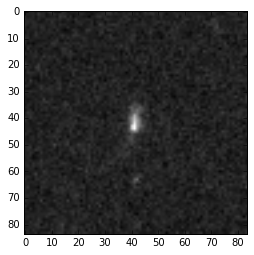
With noise removed:
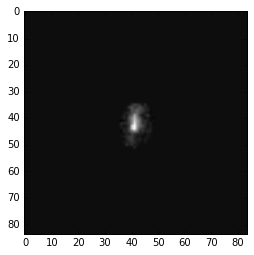
Copy the values from these pages as string s in the code below to run it locally:
from scipy.optimize import fmin
import StringIO
# get segmap and image (The text is VERY long)
segmap = np.loadtxt(StringIO.StringIO("""
PASTE segmap FILE CONTENTS HERE
"""))
img = np.loadtxt(StringIO.StringIO("""
PASTE img FILE CONTENTS HERE
"""))
#remove noise
img[segmap==0] = 0.0
# get the measured surface brightness profile
_, y = get_surface_brightness_profile(img)
# get the fit parameters
m = 1.0
init_Ie_Re = [1.0, 0.3]
opt_vals = fmin(sersic_optimize, init_Ie_Re, args(m, y))
# The returned values should be [0.01934633, 0.24175975]
Graph of the measured surface brightness profile against the fitted surface brightness profile
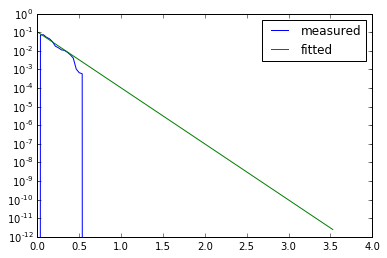
Seems to fit the data. The quick drop-off is because we cut out the noise.
Here is a graph of the fitted values for spheroid and disk.
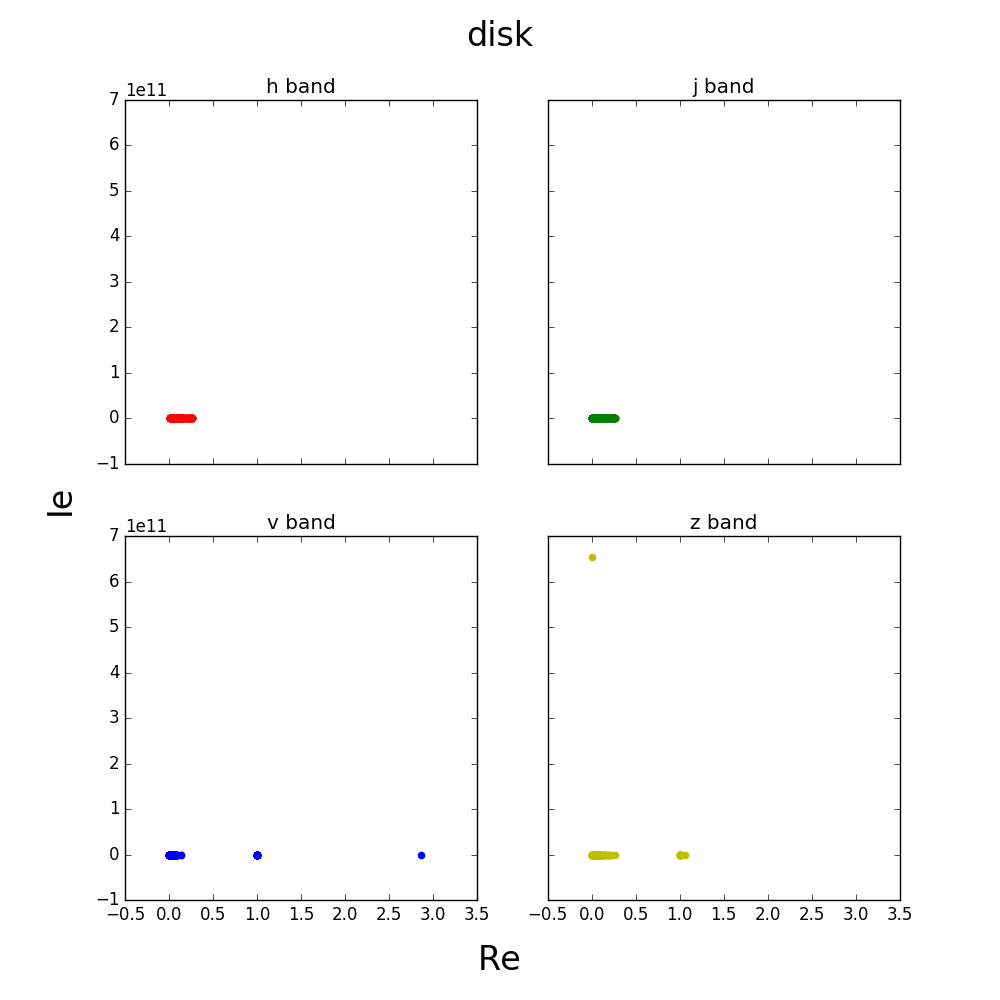
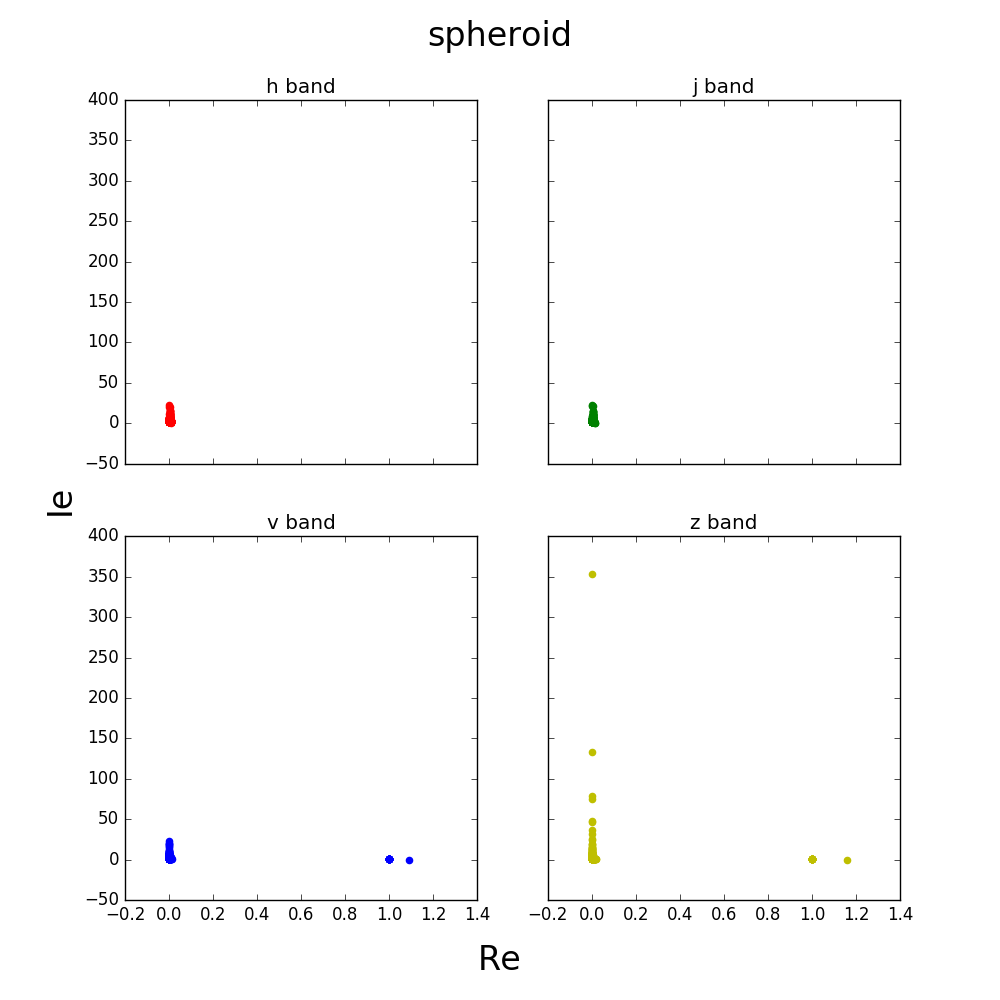
Some of the values seem to be outliers, here is a closer view of the graph.
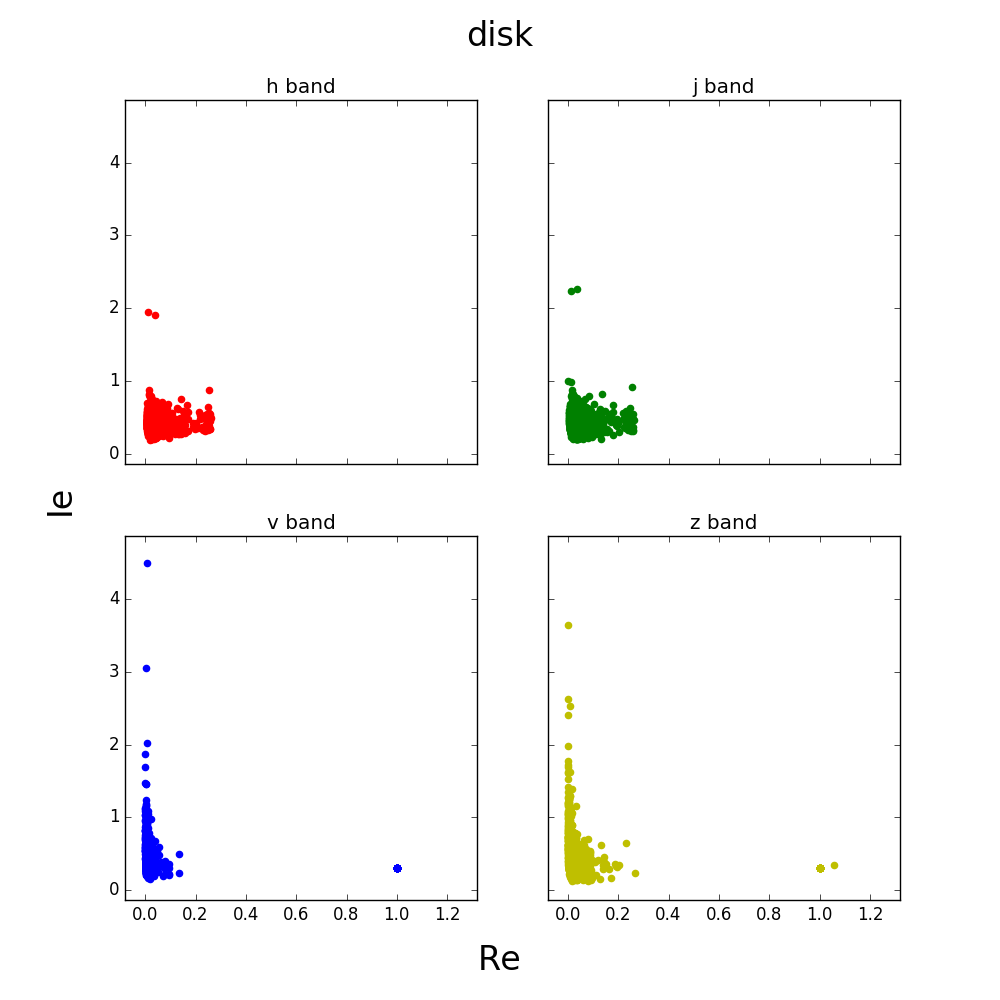
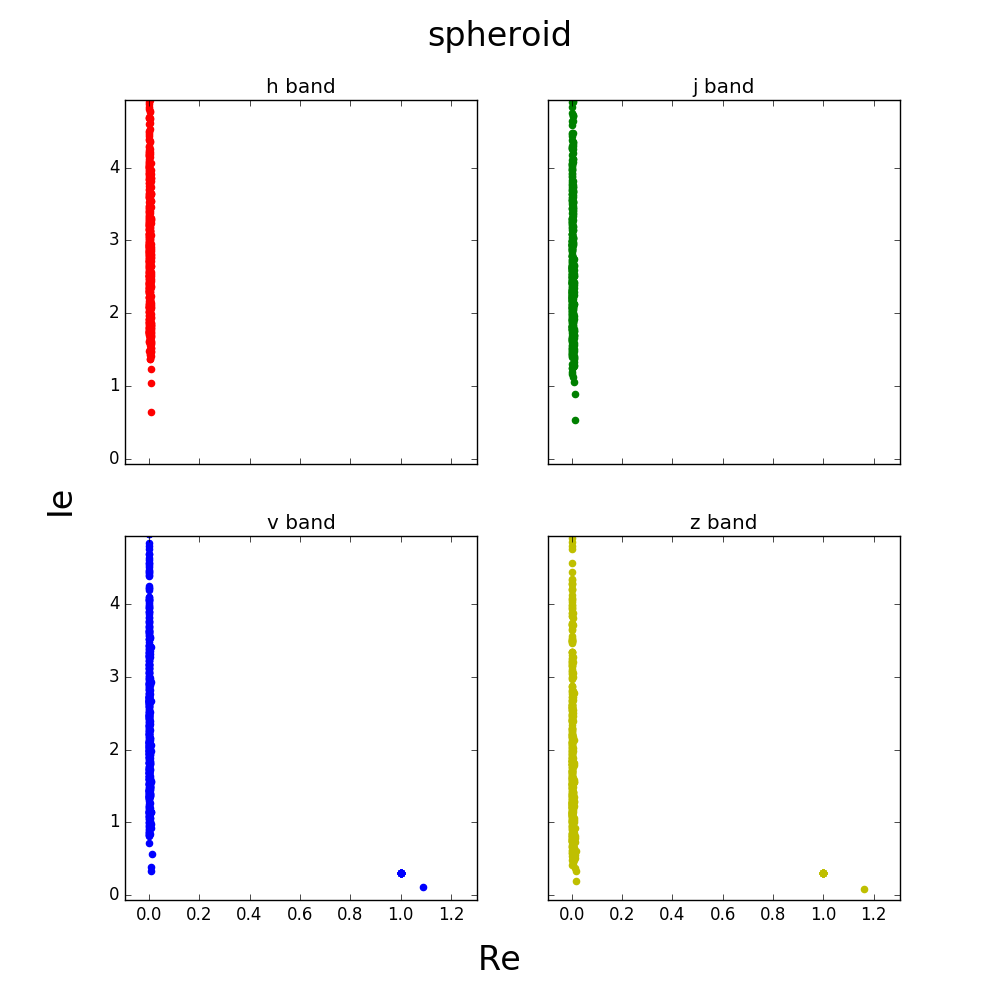
These graphs seem to make sense considering the morphology.